
Recourir à des recherches scientifiques reposant sur des données probantes présente une garantie d’objectivité et de sérieux pour les pédagogues se souciant de proposer à leurs élèves un enseignement de qualité. La publication de Lacombe, N., De Chambrier, A.-F. et Dias, T. (2021), intitulée Des données probantes au service de l’enseignement différencié des mathématiques, relève de ces préoccupations et, par conséquent, a retenu toute notre attention.
DE L’IMPORTANCE DES MATHÉMATIQUES
De l’école primaire à la vie d’adulte, les mathématiques jouent un rôle de prédicteur du succès et sont un facteur d’estime de soi. Les auteur.e.s de l’article le rappellent et se proposent d’effectuer un état des lieux des bonnes pratiques pédagogiques mises en évidence par les recherches actuelles. Étant donné que la majorité des études paraissent en langue anglaise, cette publication se donne également un rôle de passeur vers le public francophone.
UNE SÉLECTION DE REVUES ET DE MÉTA-ANALYSES
Le recours à trois bases de données leur a fourni 69 revues de littérature et de méta-analyses consacrées à l’enseignement des mathématiques. Les auteur.e.s en ont sélectionné 10, desquelles elles ont extrait différentes bonnes pratiques.
Rappelons ici que les méta-analyses recourent au concept de taille d’effet. “En statistique, une taille d’effet est une mesure de la force de l’effet observé d’une variable sur une autre. […] Le d de Cohen ou d’ permet de caractériser la magnitude d’un effet associé dans une population donnée par rapport à une hypothèse nulle. Traditionnellement, un d autour de 0.2 est décrit comme un effet « faible », 0.5 « moyen » et 0.8 comme « fort ».” (Wikipédia)
L’ENSEIGNEMENT EXPLICITE
L’enseignement explicite apparaît en tête des bonnes pratiques validées par les recherches. Rappelons que l’enseignant y joue un rôle central. C’est elle/lui qui présente la matière de manière structurée pour permettre à l’élève d’acquérir progressivement des compétences en partant des plus simples aux plus complexes, évitant ainsi toute surcharge cognitive. Les auteur.e.s citent la méta-analyse de Gersten, Chard et al. (2009) dans laquelle la taille d’effet moyen de ce type d’enseignement est très important (d = 1.22).
FEEDBACKS ET DÉMARCHE D’AUTO-QUESTIONNEMENT
Donner régulièrement des rétroactions (feedbacks) aux élèves et des rétroactions explicites quand les réponses sont inexactes constitue un élément majeur de tout bon enseignement. Quand il est pratiqué avec bienveillance et souci de faire progresser l’élève, il invite celui-ci à adopter une démarche d’auto-questionnement. L’importance d’un passage d’une appréciation extérieure vers l’intériorisation par l’élève d’une pratique d’autocritique est mise en évidence par les effets d’ampleur mentionnés dans l’étude : ils passent de 0.23 pour les feedbacks à 1.45 pour l’auto-questionnement et notamment quand il s’agit de résolutions de problèmes.
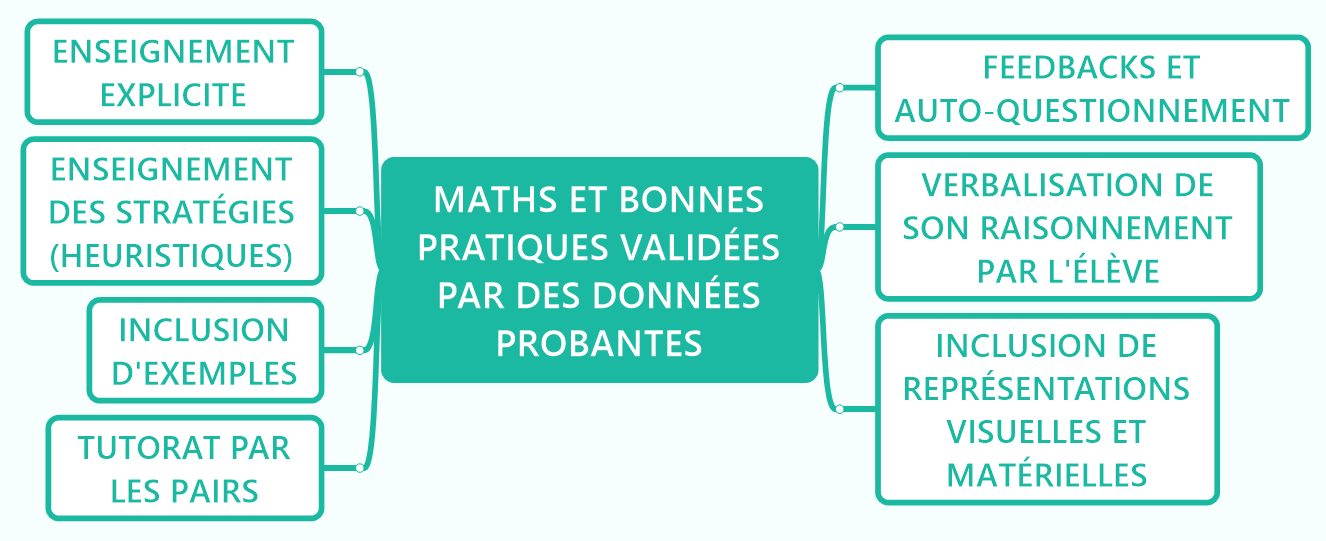
ENSEIGNEMENT DE STRATÉGIES (UTILISATION D’HEURISTIQUES)
Les effets de l’enseignement de stratégie sont multiples et potentiellement puissants puisqu’ils peuvent atteindre un effet d’ampleur de 2.36, notamment pour les élèves dyscalculiques.
Dans l’article, les auteur.e.s donnent des exemples dont RUN, TOTAL et DIFFERENCE, tirés de l’étude de Gersten, Beckman et al. (2009). Dans notre article de blog de septembre 2021, nous citions quatre propositions d’aide à la résolution de problème qui se trouvent synthétisées dans le schéma ci-dessous.

UTILISATION DE REPRÉSENTATIONS VISUELLES ET MATÉRIELLES
Quand l’enseignant parvient faire comprendre à ses élèves qu’il existe un lien entre les représentations symboliques propres aux mathématiques et d’autres représentations visuelles ou matérielles, il leur facilite la vie. Il arrive à mieux communiquer avec eux, leur permet de mieux comprendre, mieux penser, exprimer avec davantage d’aisance ce qu’ils comprennent ou, au contraire, ce qui leur reste encore hermétique. Efficace pour la résolution de problèmes, ce type d’aide présente l’avantage, une fois maîtrisée, de pouvoir s’appliquer à d’autres situations que celle initialement résolue.
Sur ce point, les auteur.e.s ne donnent pas de taille d’effet mais citent à la fois des sites susceptibles de proposer des ressources concrètes ainsi que trois publications qui soulignent l’importance de cet outil : Gersten, Chard et al. (2009), Germain Colombiès et Lafay (2021), Gersten, Beckman et al. (2009)
VERBALISATIONS PAR LES ÉLÈVES DE LEUR RAISONNEMENT MATHÉMATIQUE
Demander aux élèves d’expliquer à leur plus proche camarade ou à l’enseignant ce qu’ils ont compris ou pas encore compris est une démarche qui facilite la représentation du concept travaillé ou de la question posée. L’enseignement explicite recommande d’y recourir lors de la pratique dirigée. Les auteur.e.s citent l’étude de Gersten, Chard et al. (2009) qui évalue la taille d’effet d’une telle pratique à 1.04.
L’INCLUSION D’EXEMPLES
Il est judicieux d’inclure des exemples dans son enseignement des mathématiques, et même des exemples de problèmes déjà résolus. Cette pratique recommandée pour les élèves du primaire permet également aux élèves du secondaires de mieux se représenter les notions étudiées, notamment quand l’enseignant prend soin de passer des exemples concrets aux représentations visuelles pour finir par les notations mathématiques abstraites.
Les auteur.e.s se réfèrent à la méta-analyse de Gersten, Chard et al. (2009) pour affirmer que cette pratique atteint un effet d’ampleur de 0.82.
Elles/ils n’évoquent pas le recours aux contre-exemples, prôné par l’enseignement explicite. L’expérience nous a pourtant démontré que ceux-ci représentent souvent une aide précieuse à la mémorisation de certaines notions. C’est particulièrement le cas lorsque l’enseignant les intègre à un modèle de Frayer.
LE TUTORAT PAR LES PAIRS
Pour atteindre une taille d’effet significative, il faudrait que les tuteurs soient des élèves plus âgés que les “tutorés” (d= 1.42). Dans le cas contraire, les mérites d’une telle pratique se révèlent plutôt moyens à faibles, écrivent les auteur.e.s.
Personnellement, j’estime que le tutorat par les pairs doit être régulièrement offert pour encourager les plus timides à s’exprimer et pour recevoir de la part de leurs semblables des explications utilisant un registre de vocabulaire qui leur est propre. Si une telle offre répond à un besoin, cela se voit. L’aspect positif de tels échanges se sent à travers l’intensité des interactions. Quand elles n’ont pas lieu ou qu’elles revêtent un caractère artificiel, rien n’empêche l’adulte d’y mettre fin et de passer à d’autres pratiques plus efficaces.
REMARQUES
Tant dans l’introduction de leur article que dans la conclusion, les auteur.e.s font état des limites qu’elles/ils perçoivent dans les méta-analyses. Elles/ils évoquent notamment l’existence de certaines pratiques pédagogiques n’ayant pas encore fait l’objet d’études ou d’études trop récentes pour être incluses dans le bouquet des recherches. Elles mentionnent à titre d’exemple le recours aux didacticiels de qualité. Et elles émettent le souhaiter de pouvoir lire bientôt de nouvelles méta-analyses intégrant ces nouveautés.
De notre côté, nous estimons que les dispositifs mis en place pour vaincre la peur des mathématiques devraient eux aussi être pris en compte dans ce type d’études potentielles. Nous avons signalé dans un blog consacré à cette problématique https://axaca.net/2020/05/vaincre-la-peur-des-mathematiques/ que son effet anxiogène avait non seulement été thématisé mais que trois scientifiques : De Vita C., Passolunghi M. C, Pellizzoni S. (2020) avaient testé et émis des conclusions quant à l’efficacité de deux dispositifs élaborés pour lutter efficacement contre la si répandue peur des maths.
CONCLUSION
Très positif, de la part des auteur.e.s, d’avoir publié cet article qui, comme elles/ils disent, a le mérite de proposer un état des lieux en français et d’encourager indirectement cette culture du recours aux données probantes. Les bonnes pratiques mises ainsi en évidence vont sans doute se répandre pour le plus grand bénéfice de tous les élèves. Nous nous plaisons à relever au passage que l’enseignement explicite se trouve non seulement validé en soi mais que plusieurs des autres bonnes pratiques mentionnées dans leur synthèse sont des éléments constitutifs de sa démarche.
PUBLICATION RECENSÉE ET CITÉES
Lacombe, N., De Chambrier, A.-F., Dias, T. (2021). Des données probantes au service de l’enseignement différencié des mathématiques, in Revue de Mathématiques pour l’école RMé No236, Nov.2021, 13-26. Genève
https://www.revue-mathematiques.ch/files/2916/3611/0336/RMe-236-Lacombe_Chambrier_Dias.pdf – Consulté le 23.12.2021
Gersten, R., Chard, D., J., Jayanthi, M., Baker, S., K., Morphy, P. & Flojo, J. (2009). Mathematics Instruction for Students With Learning Disabilities: A Meta-Analysis of Instructional Components. Review of Educational Research, 79(3), 1202–1242
De Vita Chiara, Passolunghi Maria Chiara, Pellizzoni Sandra: Math anxiety and math achievement: The effects of emotional and math strategy training, March 2020.
Sur le site de Wiley Online Library : https://doi.org/10.1111/desc.12964
Buxton, L. (1981). Do You Panic About Maths? Coping with Maths Anxiety, pp. 115–117, London: Heinemann Educational Books
O’Leary, K., Fitzpatrick, C.L. and Hallett, D. (2017) Math Anxiety Is Related to Some, but Not All, Experiences with Math. Front. Psychol. 8:2067. doi: 10.3389/fpsyg.2017.02067
Park, Daeun & Ramirez, Gerardo & L Beilock, Sian. (2014). The Role of Expressive Writing in Math Anxiety. Journal of experimental psychology. Applied. 20. 10.1037/xap0000013.
