La première conclusion à en tirer, c’est qu’il est hautement profitable aux élèves de leur apprendre comment bien résoudre les problèmes mais qu’il vaut mieux éviter de compter sur les situations de problèmes à résoudre pour les faire progresser rapidement et efficacement dans leur acquisition de nouvelles compétences.
A la lecture d’études consacrées à ce sujet, on peut conclure qu’élèves et enseignants ont tous deux leur rôle à jouer et leurs tâches à remplir pour que l’exercice produise ses meilleurs effets.
CE QU’IL REVIENT À L’ENSEIGNANT : COMMENCER PAR ANTICIPER.
L’adulte référent doit prendre conscience que proposer un problème ne se fait pas à la légère. Cela nécessite au contraire une planification qui repose sur une analyse à priori. Cette analyse « permet à l’enseignant d’avancer des hypothèses à propos :
1. Des démarches, des stratégies et des procédures que les élèves utiliseront
2. Des obstacles qu’ils rencontreront et des erreurs que ceux-ci engendreront
3. De l’organisation pédagogique qui favorisera l’apprentissage dans la classe
4. Des interventions à mettre en place qui favoriseront l’apprentissage.
C’est dire que, dans son analyse a priori, l’enseignant pourra prévoir certaines variantes au problème afin de le complexifier ou de le simplifier. Ces variantes peuvent se traduire par une question, l’ajout ou le retrait d’une contrainte, la diminution ou l’augmentation de la taille des nombres, un changement de type de nombre, etc. » (Charnay, 2003, cité par Cabot Thibault, J. et Dumas, B., 2020).
IMPORTANCE DE LA FORMULATION DES ÉNONCÉS PAR LE MAÎTRE ET DE LA MAÎTRISE DES MOTS PAR LES ÉLÈVES
Expert dans sa matière, l’enseignant doit se souvenir que le jargon de la discipline doit avoir été expliqué aux élèves et appris par leurs soins. De son côté, il veillera à ce que l’énoncé des problèmes soit toujours d’une grande limpidité, d’une grande clarté, en éliminant au maximum les ambiguïtés ou les implicites qui ne sont évidents que pour les experts.
IMPORTANCE DE L’EXPLICITATION DU CONTRAT DIDACTIQUE
L’enseignant disposant d’un énorme pouvoir sur les élèves, à savoir de les évaluer et, par conséquent, d’influencer sur leur avenir scolaire et professionnel, il est important qu’il fasse explicitement le lien entre les tâches proposées et l’évaluation. Aura-t-elle lieu en continu ? Va-t-il corriger tout de suite les problèmes à résoudre. Ne le fera-t-il au contraire, qu’à partir du moment où il aura effectué corrections, commentaires et suggestions d’aide à l’apprentissage et à la mémorisation des compétences fraîchement acquises ?
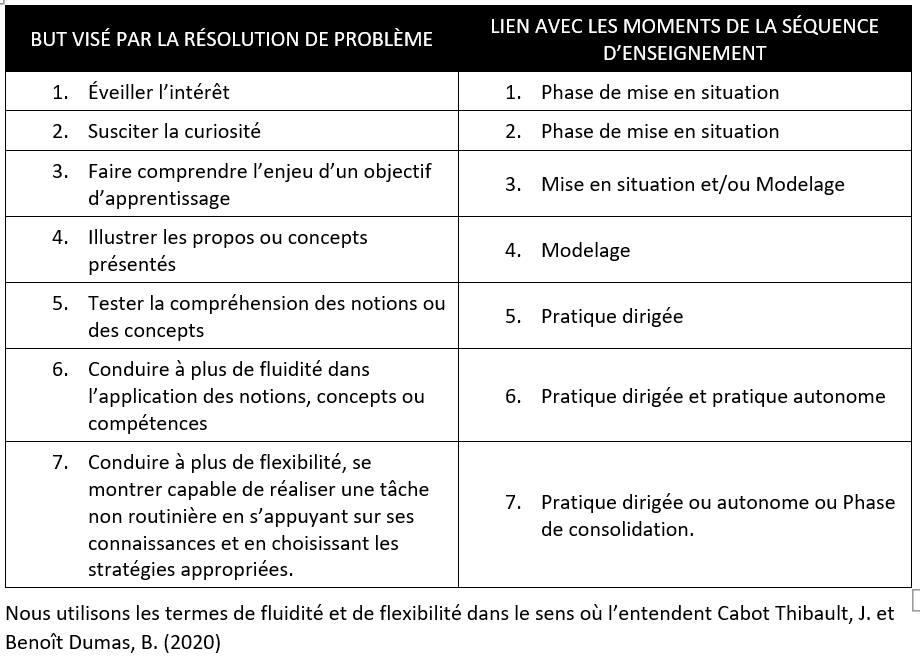
LIEN ENTRE LES PROBLÈMES ET LES MOMENTS DE LA SÉQUENCE D’ENSEIGNEMENT
Pour éviter de générer un stress inutile, l’enseignant doit expliciter les liens ci-dessous. Il est indispensable que l’élève comprenne s’il peut s’exprimer de manière spontanée, en s’autorisant des erreurs ou s’il doit réfléchir à deux fois avant d’écrire ou parler, en se remémorant ce qui a été enseigné, en démontrant ce qu’il commence à progressivement ou à parfaitement maîtriser.
CE QU’IL REVIENT À L’ÉLÈVE : COMMENCER PAR BIEN COMPRENDRE LA TÂCHE
Pour bien comprendre la tâche, il faut d’abord bien comprendre la signification des mots.
L’élève doit être conscient du fait que la langue utilisée dans l’enseignement n’est pas toujours tout à fait la même que celle de la vie de tous les jours.
Il doit aussi avoir retenu qu’il existe des synonymes qui, dans le fond, renvoient à la même idée. L’expression « Effectue la somme de… » peut figurer en toutes lettres dans l’énoncé mais aussi se trouver dans les prépositions, conjonctions de coordination, adverbes utilisés. Exemple : sachant que Bob a acheté un un premier objet à 50 .-, un deuxième à 35.- et un troisième à 17.-, combien doit-il débourser en arrivant à la caisse ? L’idée de somme à effectuer est bien présente, comme elle peut l’être lorsque son utilisé les mots « plus », « au total », « en tout… »
APRÈS LE SENS DES MOTS, CELUI DES PHRASES, POUR FAIRE LE LIEN AVEC LE CONTEXTE.
Le sens des mots varie selon les phrases et le contexte dans lequel ils sont utilisés. L’élève doit s’exercer à effectuer ce lien ô combien important.
FAIRE LE LIEN ENTRE LA TÂCHE DEMANDÉE ET LES NOTIONS MATHÉMATIQUES ÉTUDIÉES
Les problèmes à résoudre ne sont pas proposés sans raisons. L’élève doit chercher à comprendre quelles sont les attentes implicites ou explicites de son enseignant, être conscient du côté potentiellement artificiel de la situation décrite.
Il doit en outre identifier les stratégies ou les types de raisonnement à utiliser.
• Me demande-t-on de repérer les ressemblances entre deux cas de figure, de dépasser ces ressemblances pour mieux identifier des différences ?
• S’agit-il de trouver les conséquences d’une problématique à partir d’une situation de départ, d’en déduire un certain nombre d’éléments ?
• Faut-il transformer des formules mathématiques en un modèle ? Ou l’inverse ?
• Dois-je partir d’un cas spécifique pour remonter à une proposition plus générale ?

LES AIDES À LA RÉSOLUTION DE PROBLÈMES
Il convient d’enseigner explicitement aux élèves une ou deux méthodes garantissant une bonne résolution de problème.
Cabot Thibault, J. et Dumas, B. (2020) proposent 3 étapes :
1. La détermination du but du problème
2. La planification des étapes à effectuer
3. La régulation, etc.
Dacey (2014) en rajoute une de plus :
1. Comprendre
2. Faire un plan
3. L’exécuter
4. Revenir au problème.
Gauthier, C., Bissonnette, S., Richard M. (2013) en ont aussi quatre :
1. Lire la question
2. Transformer la question en « Qu’est-ce que je cherche ? »
3. Survoler le texte afin de repérer l’information
4. Comparer l’information trouvée à la question posée.
Pour Vianin, P. (2020) il y en a cinq :
1. La lecture et la compréhension du problème
2. La représentation de la situation problématique
3. La résolution effective du problème
4. L’exécution des opérations
5. L’évaluation du résultat obtenu.
CONSEILS PRATIQUES ET ASTUCES
Pour mieux comprendre la consigne et les enjeux d’un problème, Dacey propose de :
• Lire à voix haute
• Reformuler ce qui est proposé
• Faire le point sur le but recherché
• Visualiser le problème.
Elle mentionne encore :
• Mimer la situation avec des objets concrets
• L’illustrer avec des images
• Estimer ce que devra être le résultat
• Travailler à plusieurs
• Échanger, communiquer.
L’élève peut, par exemple, prendre des notes, expliquer sa démarche ou écouter les autres.

MOT DE LA FIN
Que ce soit pour la réussite en milieu scolaire ou dans sa vie en général, les mathématiques jouent un rôle très important. Il est donc primordial que chaque élève puisse bénéficier d’un enseignement de qualité, placé sous le signe de la bienveillance et de l’excellence pédagogique.
Tout enseignant.e de maths doit prendre conscience des responsabilités qui lui reviennent d’apprendre à ses élèves comment aborder cette discipline avec la bonne méthode.
En guise de conclusion, nous empruntons à Pierre Vianin (2020), la phrase prononcée par une jeune élève qui venait d’apprendre les stratégies à utiliser :
« Je vais m’appliquer à mieux penser ce que je pense »
Gaëlle, citée par Vianin, P. (2020), p. 352
BIBLIOGRAPHIE
Bütikofer, M. & Dupuis, M. (2015). Les étayages dans l’enseignement explicite en résolution de problèmes pour les élèves à besoins particuliers. Mémoire professionnel – HEP – Lausanne
Cabot Thibault, J. & Dumas, B. (2020). Définir le premier palier d’intervention en mathématiques sous l’angle des apprentissages à réaliser par l’élève et d’une pratique pédagogique à privilégier par l’enseignant. Enfance en difficulté, volume 7, mai 2020, L’approche de la réponse à l’intervention et la prévention des difficultés d’apprentissage à l’école, Université Laurentienne, Sudbury, 81-105.
Dacey, L. (2014). 100 problèmes mathématiques gradués. Montréal : Chenelière éducation
Gauthier, C., Bissonnette, S., Richard, M., Castongay, M. (2013) : Enseignement explicite et réussite éducative. La gestion des apprentissages. Montréal, Bruxelles : ERPI, de Boeck.
Vianin, P. (2020). Comment donner à l’élève les clés de sa réussite ? L’enseignement des stratégies d’apprentissage à l’école. Louvain-la-Neuve : De Boeck Supérieur
