
De manière intuitive et spontanée, tout.e enseignant.e possédant un minimum d’éthique professionnelle fait en sorte qu’un maximum d’élèves comprenne la matière des cours et se l’approprie. D’avance, l’enseignant.e sait qu’un certain pourcentage de participant.e.s devront bénéficier de davantage de temps ou d’explications pour atteindre le niveau atteint par la majorité du groupe-classe. L’enseignant.e, enfin, prévoit de proposer des appuis nettement plus spécifiques et individuels pour une minorité d’élèves qui n’auront toujours pas maîtrisé les contenus. Sans forcément le savoir, cet.te enseignant.e applique une pratique pédagogique que l’on appelle « réponse à l’intervention » ou RAI.
Les trois niveaux de la RAI correspondent aux 3 temps décrits ci-dessus et représentés dans le schéma ci-dessous. Leur but est de lutter efficacement contre les difficultés en milieu scolaire, qu’elles soient liées au comportement, à la littératie ou à la numératie.
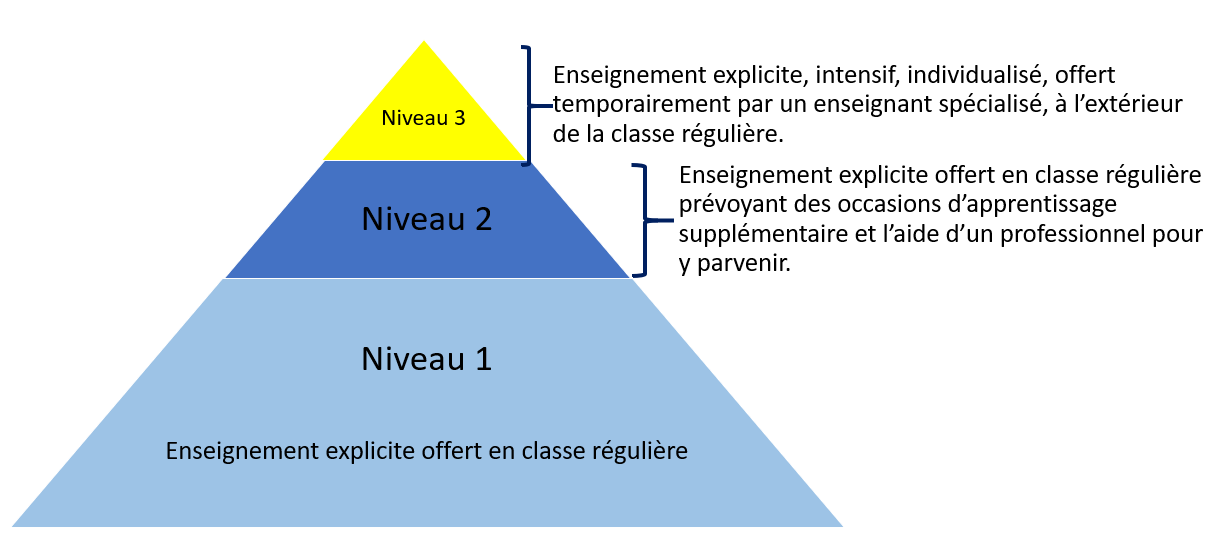
Des chercheurs tels que Hattie (2017), Burns, Appleton & Stehouwer (2005) ont validé les effets très positifs de la RAI. Hattie cite une méta-analyse démontrant un effet d’ampleur de 1,07. Quant à Burns, Appleton & Stehouwer, ils affirment que la RAI amène une diminution du nombre d’élèves en grandes difficultés scolaires de 5,2% à 2%.
Dans cet article, nous allons voir ce que deux spécialistes de la RAI, Jim Cabot Thibault et Benoît Dumas, recommandent en matière d’intervention de niveau 1 à propos de l’enseignement des mathématiques (cf. schéma ci-dessus et référence bibliographique en fin de texte).
En s’appuyant sur des publications scientifiques, les deux auteurs soulignent l’importance de trois dimensions communes à toutes les notions enseignées dans les cours de maths : la compréhension conceptuelle, la fluidité et la flexibilité.
COMPRÉHENSION CONCEPTUELLE
Les auteurs la définissent comme étant le « quoi » et le « pourquoi » d’un concept. L’élève qui maîtrise la compréhension conceptuelle va progressivement se montrer capable d’effectuer des liens entre les concepts et la réalité mais aussi entre les différents concepts eux-mêmes. Cette maîtrise rendra possibles des transferts de la théorie à des situations problèmes ou à des applications concrètes. Se sentant capable de les opérer, l’élève prendra conscience du sens et de l’utilité du concept mathématique étudié. Sa motivation à le garder en mémoire et à en étudier d’autres s’en trouvera ainsi renforcée.
FLUIDITÉ
Comprendre un concept n’est qu’un début. Il s’agit ensuite de se l’approprier, de se montrer capable de l’utiliser. On passe alors de la compréhension à la connaissance. À un premier type de connaissance maladroite et hésitante doit succéder une maîtrise de grande aisance puis un sur-apprentissage permettant un maximum d’automaticité. Les automatismes, rappelons-le, libèrent la mémoire de travail, permettent de consacrer davantage d’attention à la résolution de tâches plus complexes.
Les auteurs donnent l’exemple d’un élève qui a compris qu’un nombre pouvait être décomposé de différentes façons. Après apprentissage et surapprentissage, cet élève devrait pouvoir se servir de cette nouvelle compétence pour effectuer de façon fluide la multiplication suivante : 24 x 8 = (20 x 8) + (4 x 8) = 160 + 32 = 160 + 30 + 2 = 192.
FLEXIBILITÉ
La flexibilité implique trois aptitudes :
- Connaître plusieurs manières d’effectuer une tâche similaire ;
- Être capable d’inventer une procédure pour réaliser une tâche non routinière en s’appuyant sur ses connaissances ;
- Parvenir à trouver la meilleure façon de réaliser une tâche.
La compréhension contextuelle et la fluidité sont étroitement liées et chacune d’elles contribue à renforcer la flexibilité.
REPÉRER ET IDENTIFIER LES FAIBLESSES POUR INTERVENIR DE MANIÈRE PLUS CIBLÉE
Face à des élèves qui rencontrent des difficultés, il est important que l’enseignant puisse identifier laquelle des trois dimensions demande à être revisitée, retravaillée, réinvestie. Il revient à l’adulte de démontrer à l’élève que « découvrir » un nouveau contenu n’est pas l’équivalent de le « comprendre ». L’enseignant doit le convaincre que la fluidité doit venir s’ajouter à la compréhension afin qu’apparaisse la flexibilité. Dans ce dialogue avec son élève, le maître l’incitera à multiplier les approches, les stratégies, les techniques d’apprentissage et de mémorisation.
DIFFÉRENTES MANIÈRES DE REPRÉSENTER UN CONCEPT MATHÉMATIQUES
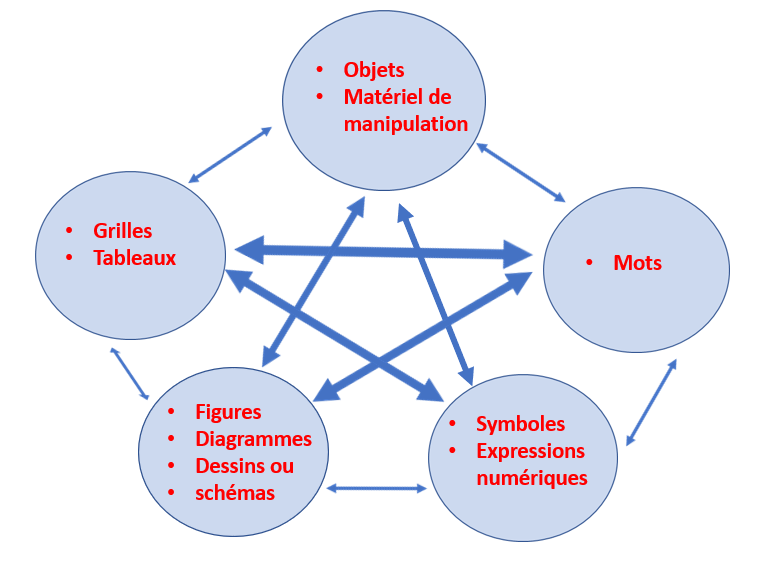
Pour se faire comprendre et pour amener les élèves à l’appropriation des nouvelles notions, l’enseignant.e de mathématiques peut se servir non seulement de mots mais encore d’expressions et de symboles numériques, de schémas, de dessins, diagrammes, figures, tableaux, grilles, voire de matériel de manipulation. Les élèves doivent pouvoir passer de l’un à l’autre de ces modes de représentation, pour faciliter leur compréhension des différentes dimensions d’un concept.
VOCABULAIRE
Le vocabulaire peut être une source d’ambiguïtés dommageables à la compréhension des concepts ou des tâches. Il est donc recommandé de lever ces ambigüités en expliquant, par exemple, la différence qui existe entre le produit à lessive et le produit d’une multiplication. Autre exemple, il n’est pas incongru d’expliquer que la division dont il est question au cours de mathématiques n’est pas l’équivalente d’une division de 15’000 hommes évoquée par l’enseignant d’histoire en parlant de deux armées qui s’affrontent.
Depuis la sortie du film « Le thé au harem d’Archimède », les profs de maths ont encore mieux saisi l’importance de proposer à leurs élèves des glossaires à conserver précieusement pour ne pas se tromper sur la signification du mot “théorème”, par exemple. Des consignes claires doivent insister sur l’importance de pareils lexiques qu’il s’agit d’enrichir au fur et à mesure de la compréhension de nouveaux termes et de nouvelles notions. Last but not least, l’élève devra bien évidemment apprendre ces mots par cœur et les retenir pour ne plus avoir de doute ni d’hésitation quand le maître annonce la présentation d’un nouveau théorème. Qu’il s’agisse de celui d’Archimède ou de Thalès…
LA VERBALISATION
En posant des questions avec bienveillance, en écoutant attentivement les réponses des élèves, en les autorisant par avance à commettre des erreurs, en se servant de ces erreurs pour reprendre les explications des notions travaillées, l’enseignant de mathématiques démontre par l’acte l’importance de la verbalisation. Il doit être le premier à mettre un haut-parleur sur sa pensée pour permettre à ses élèves de suivre son raisonnement. Mais il n’en a pas l’exclusivité. Les élèves doivent s’y exercer eux aussi, que ce soit en répondant à l’enseignant ou en se livrant à des échanges avec leurs pairs. De tels moments d’échanges sont à prévoir dans les cours, notamment en demandant aux élèves de travailler par deux. Ces instants de dialogue n’ont pas besoin d’être longs pour déployer leurs effets positifs : avoir la liberté de parler sans gêne à un camarade, de bénéficier ou de le faire bénéficier d’une compréhension, d’une stratégie différente, oser une hypothèse, prendre le risque de commettre une erreur, pouvoir s’en servir afin de mieux comprendre la spécificité du nouveau concept à apprendre et à maîtriser.
LES STRATÉGIES COGNITIVES ET MÉTA-COGNITIVES
On l’a vu ci-dessus, les stratégies pour apprendre, comprendre, retenir, travailler la fluidité et la flexibilité sont diverses et variées. Telle technique, tel outil qui conviendra à l’un n’aura que peu d’effets sur un autre. Les élèves doivent en prendre conscience avec l’aide de leur enseignant pour mieux se donner ensuite la liberté de choisir ce qui leur est le plus utile et… l’utiliser.
LA RÉSOLUTION DE PROBLÈMES
La résolution de problèmes est considérée par différents chercheurs, dont Hattie, comme un bon moyen d’entraîner la compréhension contextuelle, la fluidité et la flexibilité.
Pour qu’elle soit profitable aux élèves, elle exige toutefois de l’enseignant qu’il prenne beaucoup de précautions.
Il doit choisir soigneusement quels types de problèmes il va proposer, prévoir de les adapter au niveau des élèves constaté en cours de réalisation, accompagner les apprenants à chacun des stades, exciter leur curiosité, donner du sens à l’exercice et, finalement, préciser les éléments principaux à retenir.
Tout ça n’est pas simple du tout mais, quand les choses sont bien faites, le succès devrait être au rendez-vous. Les analyses et méta-analyses démontrent un grand effet d’ampleur obtenu par les résolutions de problèmes qui contribuent à renforcer chacun des trois domaines énumérés en début de cet article.
RAPPEL
La pédagogie qui s’appuie sur le modèle de la Réponse à l’intervention (RAI) recommande à l’enseignant d’être tout particulièrement investi dans la préparation et dans la dispensation de ses cours, ceci pour qu’un maximum d’élèves comprenne le contenu diffusé et se l’approprie durablement.
Cette pédagogie implique également un pari d’éducabilité dont bénéficient tous les élèves, notamment lorsqu’il s’agit du premier niveau d’intervention et cela au nom d’un état d’esprit forcément bienveillant et démocratique.
La RAI a pour principe de se référer à des études fondées sur des données probantes, raison pour laquelle les notions ci-dessus – qui répondent à ce type d’exigence – revêtent une importance toute particulière.
LES LIGNES CI-DESSUS SONT UNE RECENSION LIBRE DE L’ARTICLE SUIVANT :
Cabot Thibault, J. & Dumas, B. (2020). Définir le premier palier d’intervention en mathématiques sous l’angle des apprentissages à réaliser par l’élève et d’une pratique pédagogique à privilégier par l’enseignant. Enfance en difficulté, volume 7, mai 2020, L’approche de la réponse à l’intervention et la prévention des difficultés d’apprentissage à l’école, Université Laurentienne, Sudbury, 81-105.
OUVRAGES CITÉS DANS CET ARTICLE :
Burns, M. K., Appleton, J. J., & Stehouwer, J. D. (2005). Meta-analytic review of responsiveness-to-intervention research: Examining field-based and research-implemented models. Journal of Psychoeducational Assessment, 23(4), 381-394. https://doi.org/10.1177/073428290502300406
Hattie, J. (2017). L’apprentissage visible pour les enseignants : connaître son impact pour maximiser le rendement des élèves. Presses universitaires du Québec. Québec.
